字数

391 字

阅读时间

2 分钟

这是求解傅里叶系数的一个重要概念。 首先正弦和余弦函数就是两个相互正交的函数。 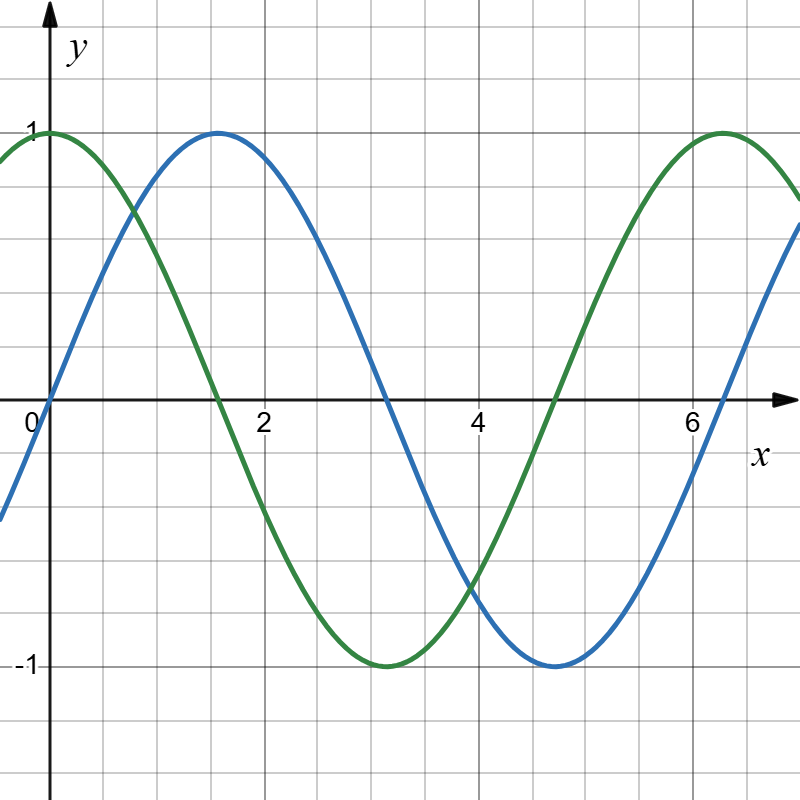这里“正交”成直角的意思，但并不是图像的几何关系，而是 sinx 与 cosx 的波形相差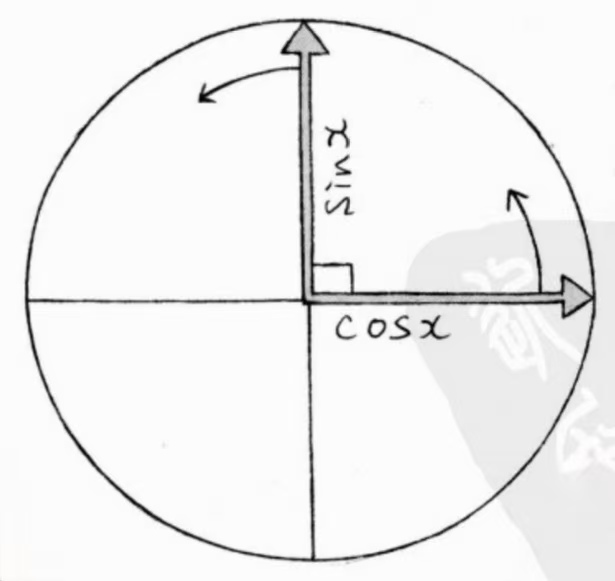 $\frac{\pi }{2}$，$\frac{\pi }{2}$ 在单位圆中正好对应的就是 90°的角度位置。

结论：如果函数成正交关系，那么它们的积的定积分为 0。

例 1：

$$y=sinx\times cosx$$

可以根据积化和差公式：

积化和差公式

$$\sin \alpha \cos \beta =\frac{1}{2}[\sin (\alpha +\beta )+\sin (\alpha -\beta )]$$

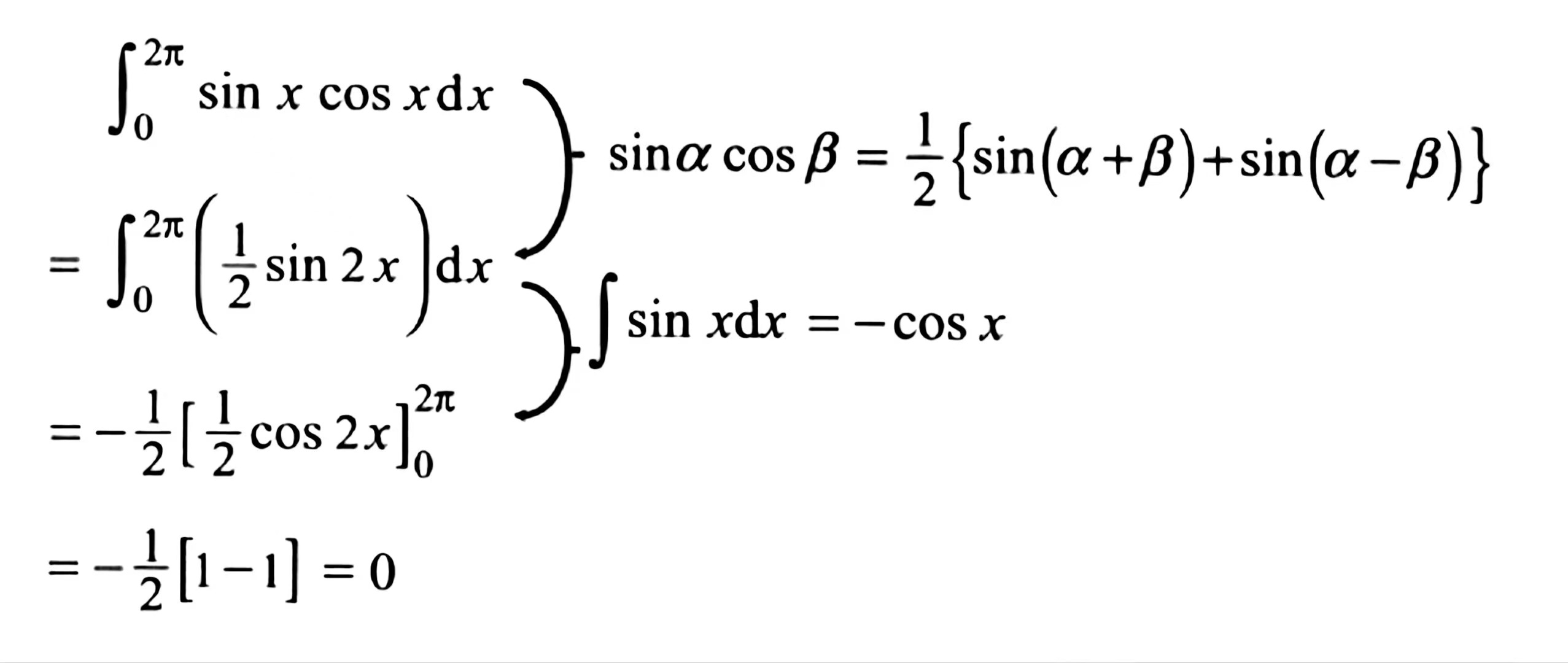
积分区间取周期长的那个函数的一个周期。

可视化展示：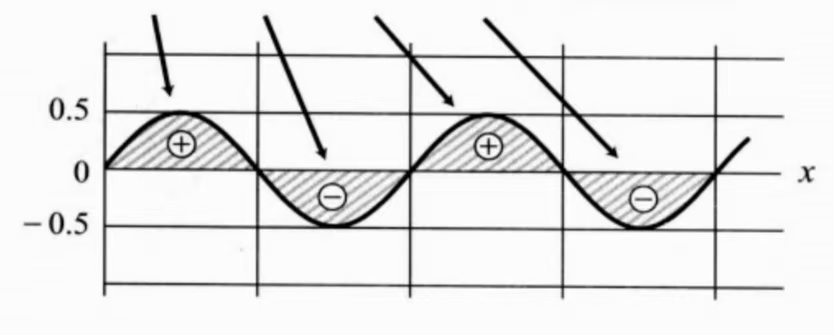

例 2：

$$y=sinx\times sin2x$$

积化和差公式

$$\sin \alpha \sin \beta =-\frac{1}{2}[\cos (\alpha +\beta )-\cos (\alpha -\beta )]$$

计算过程：

$${\int }_0^{2\pi }\sin x\cdot \sin 2xdx=\frac{1}{2}{\int }_0^{2\pi }(\cos x-\cos 3x)dx$$$$=\frac{1}{2}({\int }_0^{2\pi }\cos xdx-{\int }_0^{2\pi }\cos 3xdx)=0$$

可视化展示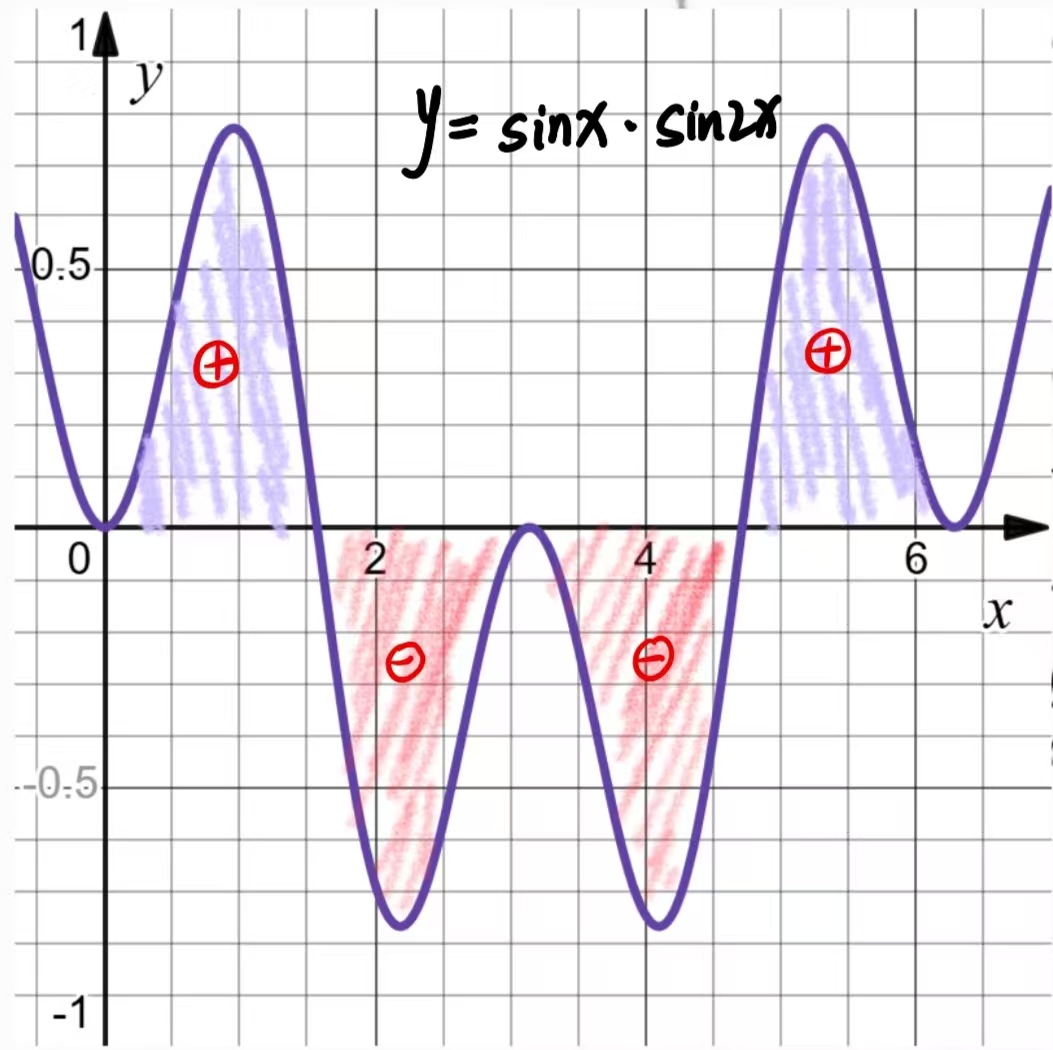： 由此得出，不同周期的正弦函数的相互成正交关系。 表示为数学语言为：

数学语言

“m, n 为不同的正数时，$sinnx$ 与 $sinmx$ 成正交关系。” 同样的，对于余弦函数也一样，$cosnx$ 与 $cosmx$ 成正交关系。 当 $m=n$ 时，$si{n}^{2}nx$ ，$co{s}^{2}nx$ 始终为正数，所以定积分结果不可能为 0，因此可以推导出, 函数与函数本身不正交。

贡献者

OveDuke

文件历史

最后编辑于 3 天前查看完整历史

75f0b-0828-2

4ab5e-0828