学完傅里叶级数后，有一种感受：看完公式后努力地记下来，记下来之后，一段时间不用，又忘记了😣，常数项表达式分母是什么？到底是哪个系数有 $\frac{1}{2}$？$a_n$ 和 $b_n$ 的表达式总是搞混。 看完这篇文章，你将明白傅里叶系数，原来是这么来的! 帮助你更深刻地理解傅里叶解析的全过程。

---

1.开篇介绍

字数

1632 字

阅读时间

7 分钟

开篇介绍傅里叶级数的展开式：

$$\begin{array}{rl}f(x)& =\frac{a_0}{2}+a_1\cos (x)+a_2\cos (2x)+\cdots +a_{n}cos(nx)\\ & +b_1\sin (x)+b_2\sin (2x)+\cdots +b_{n}sin(nx)\\ & =\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos (nx)+b_n\sin (nx)]\end{array}$$

这个式子看起来很复杂，接下来让我们分析这些系数都代表什么，以及它们的计算方法。

2.为什么要有傅里叶级数？

傅里叶级数可以用来表示周期函数。 通过对 sin 和 cos 的组合，可以得到许多不同形状的波形，可以看看下面的两种组合：

$$sinx+sin2x+sin3x$$

$$sinx+0.5cos3x+0.5sin3x$$

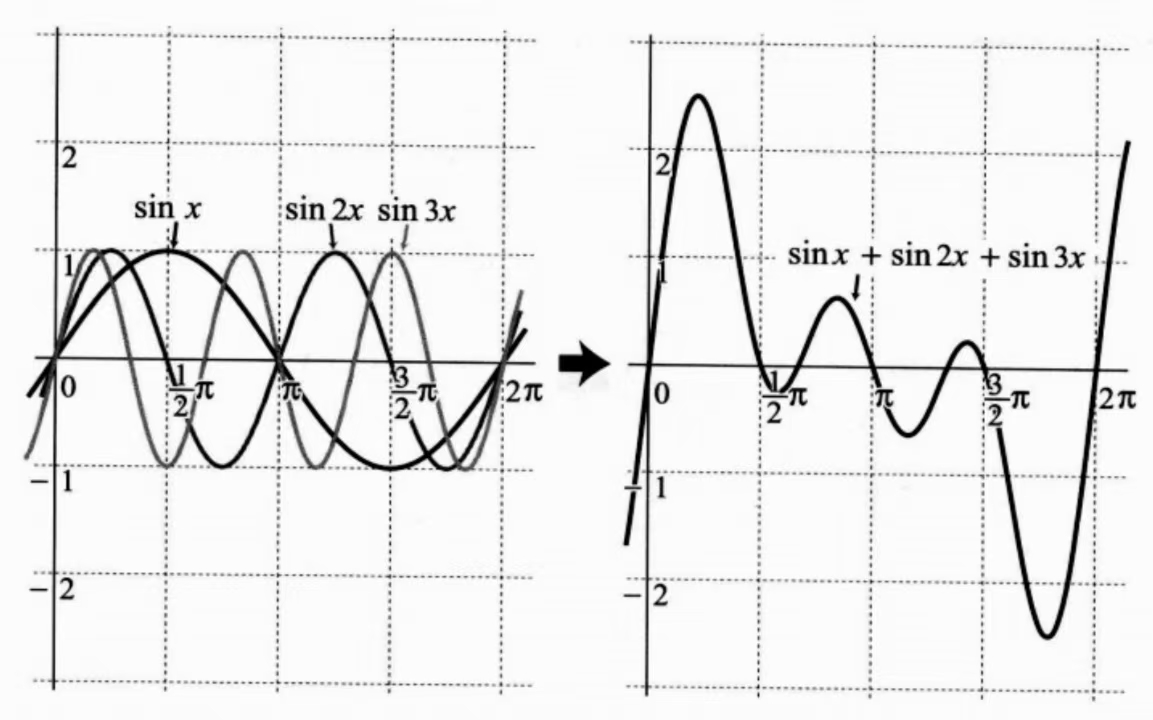
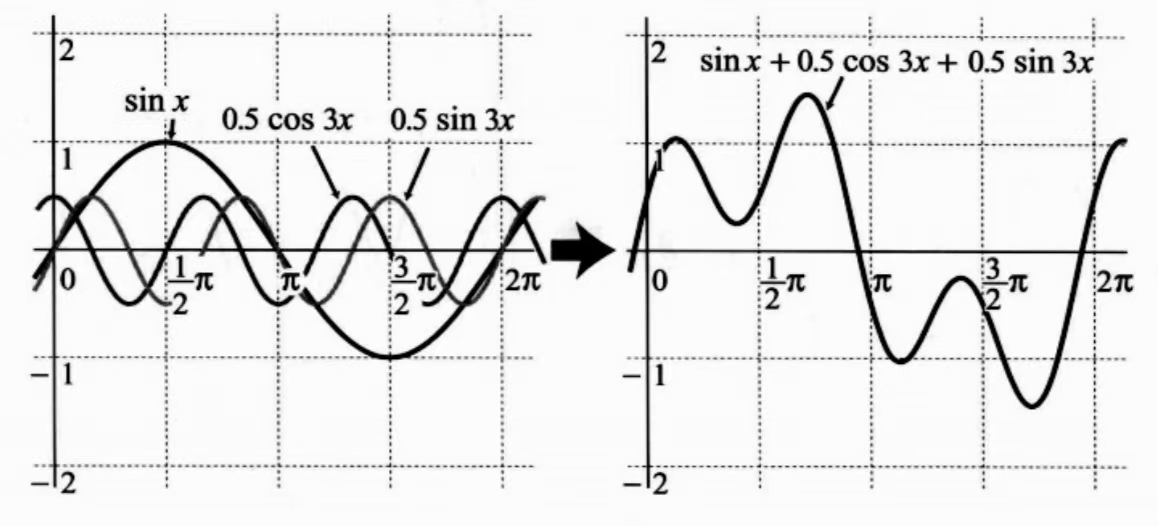
sin 和 cos 都是周期函数，通过不同的系数线性组合，得出的函数依然周期函数。 因此，自然现象中的波形如果是非周期函数，可以只截取其中一段，然后重复拓展到整个区间，仍然是周期函数，也可以用傅里叶级数来表示。

图非周期函数周期化（参考《漫画傅里叶解析》）

这就是傅里叶级数的特点：将多个周期函数合成为一个复杂的波形。

3.傅里叶变换与傅里叶级数有什么关系？

对于这样一种复杂的函数，在时间域中看起来很复杂，如果只看波形，甚至不知道原来是由哪些频率成分组成的，但是如果想要在频率域中表示，成分就很清晰了。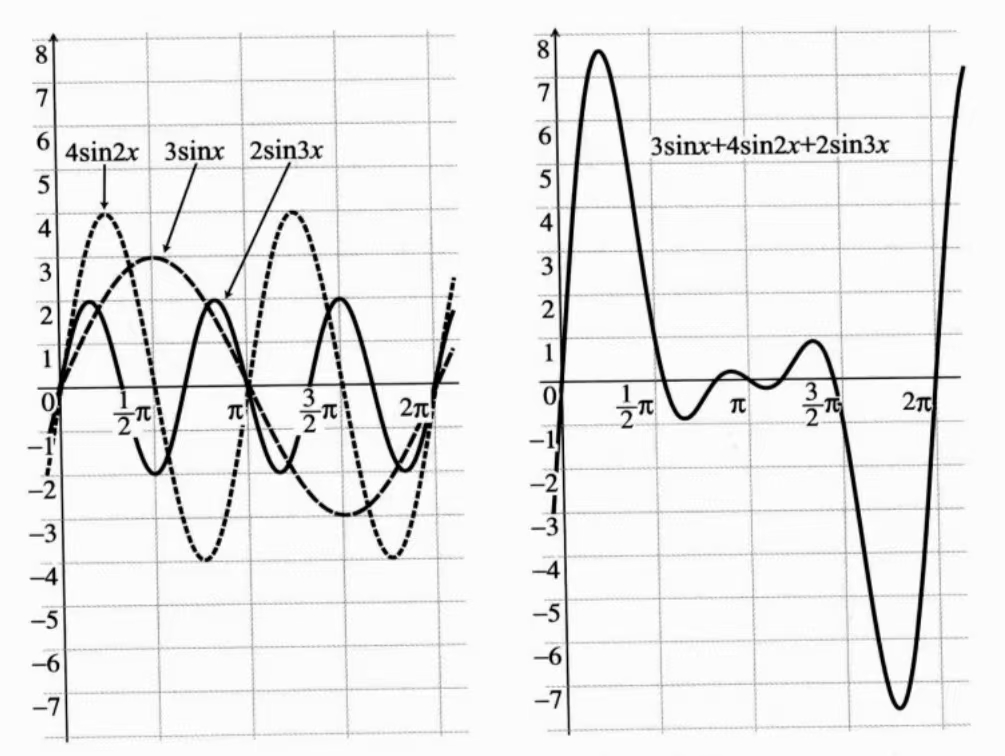

如果以频率为横坐标，频率成分的幅值为纵坐标，把它们组合的函数转化为频率谱图像如下，可以明确的的看出来这个波形由哪些频率成分组成，它们分别的幅值是多少。

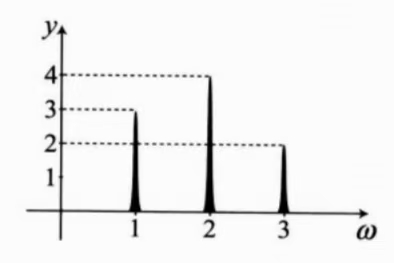
求解频率成分的这个过程就是傅里叶变换。

因此傅里叶变换的特点是：从一个复杂的周期函数分解出各个函数的周期和大小。

傅里叶级数和傅里叶变换之间的关系，简单来说，就是合成与分解的关系。

傅里叶解析，就是根据傅里叶级数的逆向思考方法，采用傅里叶变换对波形进行分析。

4.傅里叶解析求解频率成分

4.1把定积分类比成滤波器？

傅里叶解析是求解原波形（函数）由哪些频率的波以怎样的大小组合而成的方法。其中需要涉及到定积分的使用，定积分就类似于使用滤波器，把相应频率的周期函数筛选出来。

因此，如果想要求解出原波形的频率成分，需要从最低的频率开始，到计算中可能出现的最高的频率，需要对所有频率一一进行分析。

这种从从原波形 $F(x)$ 中求解出傅里叶级数中的 $a_0,a_n,b_n$ 的过程叫做“求解傅里叶系数”。

4.2 抽取频率成分系数$a_n,b_n$

根据之前发过的一篇文章，了解到函数正交是傅里叶解析的一个重要概念，参考上一篇文章：函数正交 1-函数的正交

$sin(nx),cos(nx)$ 都与自身不成正交关系，因此想要得到哪一部分频率成分的系数，可以将 $F(x)$ 全体乘以该频率成分的三角函数, 然后做定积分即可。

---

例如：如果想要得到 $a_{n}cos(nx)$ 对应的系数，只需要将 $F(x)$ 全体乘以 $cosnx$, 然后做定积分，其余频率项都与 $cos(nx)$ 正交，因此只剩下一项：

$${\int }_0^{2\pi }{a}_{n}cos(nx)\cdot cos(nx)$$

根据积化和差公式：

$$\cos \alpha \cos \beta =\frac{1}{2}[\cos (\alpha +\beta )+\cos (\alpha -\beta )]$$

可以得到：

$$\begin{array}{rl}{\int }_0^{2\pi }\cos (nx)\cos (nx)dx& ={\int }_0^{2\pi }\frac{1}{2}[\cos (2nx)+1]dx\\ & =\frac{1}{2}(0+2\pi )=\pi \end{array}$$

因此可以得出系数 $a_n$ 的表达式：

$$a_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(nx)dx$$

同理，系数 $b_n$ 的表达式为：

$$b_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)sin(nx)dx$$

---

4.3 常数项的含义及其求解

对于一个周期函数或者周期延拓的非周期函数，可以表示为$sin$和$cos$的组合。而这些三角函数，在整个周期内它们的图形围成的面积都应该是0。

如果对于一个复杂的波形在周期内求定积分，得到的结果不为0，这个结果可以用一个常数项在表示，面积为 $a_0\cdot 2\pi$。

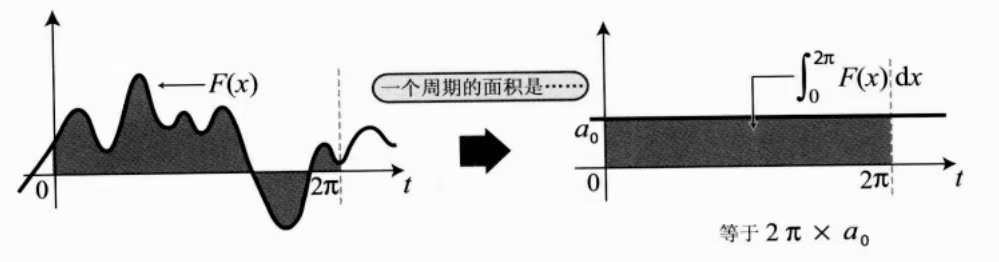
因此这个常数项为：

$$a_0=\frac{1}{2\pi }{\int }_0^{2\pi }F(x)dx$$

但是，为了统一公式，希望 $a_0$ 的求解过程可以与 $a_n$ 的求解保持一致，

$$a_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(nx)dx$$

所以当 $n=0$ 时，

$$a_0=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(0)dx$$

因此在傅里叶级数中，常数项应该表示为 $\frac{a_0}{2}$, 这样才能保证常数项的值正确。

因此，通过这样的可视化理解，我们就能对傅里叶系数的求解公式有更深的认识了，最后再总结一下：

傅里叶系数求解公式总结：

$$\begin{array}{rl}{a}_n& =\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(nx)dx\\ b_n& =\frac{1}{\pi }{\int }_0^{2\pi }F(x)sin(nx)dx\\ a_0& =\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(0)dx\end{array}$$

5.利用系数表示出频率谱

如果要表示成频率谱，则需要求解各个频率成分的大小，就是它们的幅值， 计算出 $r_n$:

$$r_n=\sqrt{a_n^2+b_n^2}$$

得到频率成分的大小以后，按照 $n$ 从小到大的顺序排列，画出图形，即可得到频率谱了。 谢谢您看到了这里！希望共同进步。 公众号内容如下，欢迎关注！ https://mp.weixin.qq.com/s/C1lxM2xqd1xPASaWsdm2ZQ

贡献者

OveDuke

文件历史

最后编辑于 大约 12 小时前查看完整历史

a86c8-0830

d9685-0830

1f7cb-Create 5-学了这么久，原来傅里叶系数是这么来的？（微信公众号）.md