根据上一节 3-傅里叶级数 知道，傅里叶解析是求解原波形（函数）由哪些频率的波以怎样的大小组合而成的方法。（反求频率成分及其幅值）

类比滤波器

字数

730 字

阅读时间

3 分钟

如果想要求解出原波形的频率成分，需要从最低的频率开始，到计算中可能出现的最高的频率，需要对所有频率一一进行分析。

从原波形 $F(x)$ 中求解出傅里叶系数中的 $a_0,a_n,b_n$ 的过程叫做“求解傅里叶系数”，这个过程就像使用滤波器的过程，将不同的频率成分逐一筛选出来。

抽取频率成分

根据之前接触到的函数正交的知识，1-函数的正交(准备知识)$sin(nx),cos(nx)$ 都与自身不成正交关系，因此想要得到哪一部分频率成分的系数，可以将 $F(x)$ 全体乘以该频率成分的三角函数, 然后做定积分即可。 例如：如果想要得到 $a_{n}cos(nx)$ 对应的系数，只需要将 $F(x)$ 全体乘以 $cosnx$, 然后做定积分，其余频率项都与 $cos(nx)$ 正交，因此只剩下一项：

$${\int }_0^{2\pi }{a}_{n}cos(nx)\cdot cos(nx)$$

根据积化和差公式：

积化和差公式

$$\cos \alpha \cos \beta =\frac{1}{2}[\cos (\alpha +\beta )+\cos (\alpha -\beta )]$$

$${\int }_0^{2\pi }\cos (nx)\cos (nx)dx={\int }_0^{2\pi }\frac{1}{2}[\cos (2nx)+1]dx=\frac{1}{2}(0+2\pi )=\pi$$

因此可以得出系数 $a_n$ 的表达式：

$$a_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(nx)dx$$

同理，系数 $b_n$ 的表达式为：

$$b_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)sin(nx)dx$$

常数项的含义与求取

对于一个周期函数，可以表示为 sin 与 cos 的组合，而对于 sin 和 cos 函数，在整个周期内它们的图形围成的面积都是 0，那么如果对于一个复杂的波形在周期内求定积分，得到的结果不为 0，则可以用一个常数项来表示，面积为 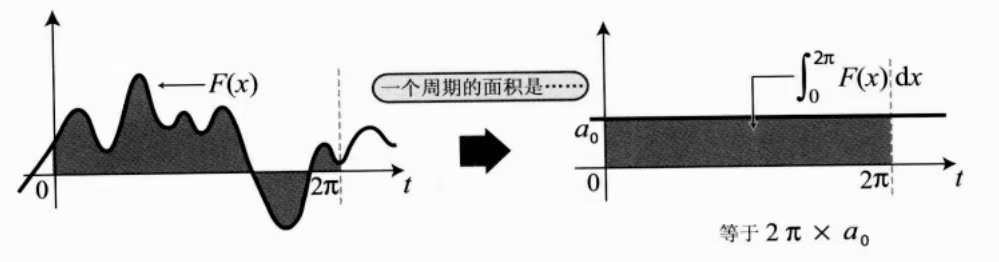$a_0\cdot 2\pi$。 因此这个常数项为：

$$a_0=\frac{1}{2\pi }{\int }_0^{2\pi }F(x)dx$$

但是，为了统一公式，希望 $a_0$ 的求解过程可以与 $a_n$ 的求解保持一致，

$$a_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(nx)dx$$

所以当 $n=0$ 时，

$$a_0=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(0)dx$$

因此在傅里叶级数中，常数项应该表示为 $\frac{a_0}{2}$, 这样才能保证常数项的值正确。

总结：

$$a_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(nx)dx$$

$$b_n=\frac{1}{\pi }{\int }_0^{2\pi }F(x)sin(nx)dx$$

$$a_0=\frac{1}{\pi }{\int }_0^{2\pi }F(x)cos(0)dx$$

频率成分大小

如果要表示成频率谱，则需要求解各个频率成分的大小 计算出 $r_n$:

$$r_n=\sqrt{a_n^2+b_n^2}$$

得到频率成分的大小以后，按照 $n$ 从小到大的顺序排列，画出图形，即可得到频率谱了。

贡献者

OveDuke

文件历史

最后编辑于 3 天前查看完整历史

75f0b-0828-2

4ab5e-0828