矩阵的建立
字数
479 字
阅读时间
2 分钟
直接输入法
中括号中各个元素用==空格或者逗号==分隔，行与行之间用==分号==分隔
特殊矩阵的建立
对角矩阵
diag() 里面可以放向量也可以放矩阵 输入向量的时候是以向量中的元素为对角线生成对角矩阵 传入矩阵时，是提取矩阵的对角线，作为向量输出。
随机矩阵
rand(4,5)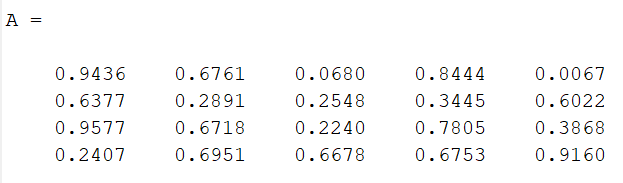
randn(4,5)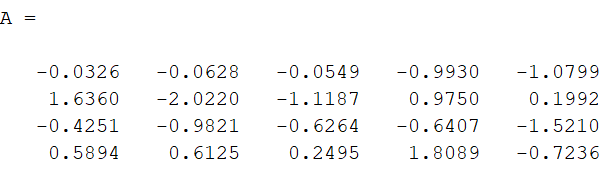
randi (4,5) 最大为 4 的随机整数，5, x 5 的方针 
多项式的伴随矩阵
matlab
% 假设有一个多项式p(x) = x^3 + 4x^2 - 7x + 10
u = [1 4 -7 10]; % 多项式的系数
compan_M = compan(u) %接受一个包含多项式系数的向量作为输入，并返回相应的伴随矩阵
% 计算伴随矩阵的特征值,伴随矩阵是由原矩阵的各个代数余子式组成的矩阵，与矩阵的逆之间有密切的联系。
values = eig(compan_M)
% 显示结果
disp('伴随矩阵的特征值（即多项式的根）为:');
disp(values)
稀疏矩阵
S = sparse(A) 通过挤出任何零元素将满矩阵转换为稀疏格式。如果矩阵包含许多零，将矩阵转换为稀疏存储空间可以节省内存。 S = sparse(m,n) 生成 m×n 全零稀疏矩阵
下面是官方文档中对稀疏矩阵的应用，建立一个一万乘一万的单位矩阵为满矩阵，与将它转为稀疏矩阵相比，他们占据的内存空间比值有 3200 倍。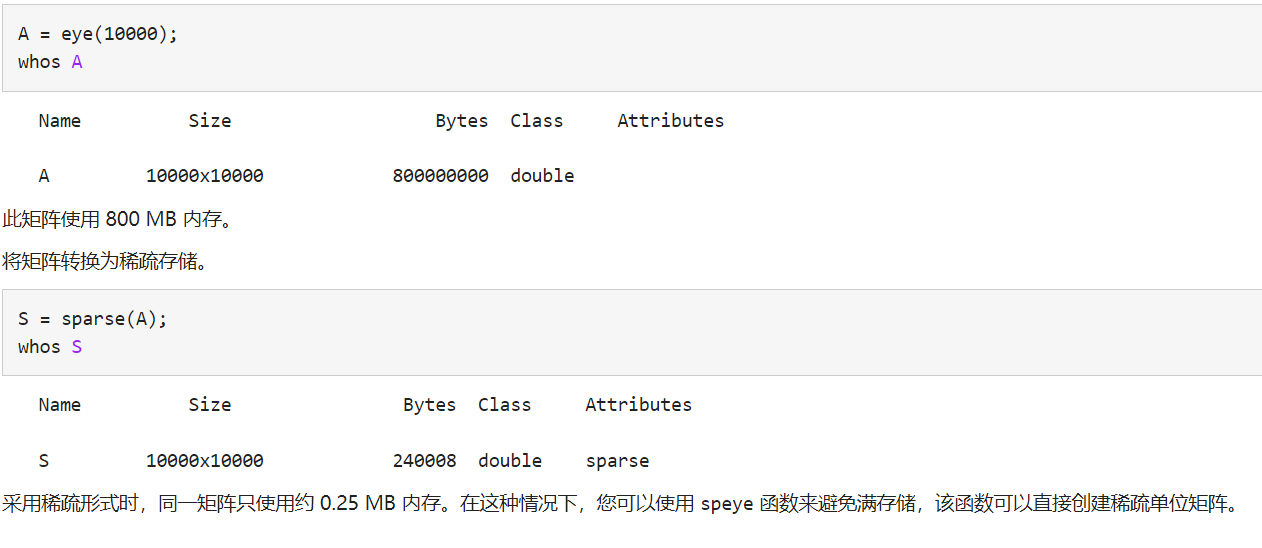 
>>edit 和使用 ctrl+N 是相同的功能
条件语句
if
switch
while
Matlab 默认参数使用双精度类型。
贡献者
OveDuke