Notebase

字数

642 字

阅读时间

3 分钟

矩阵向量的乘法

看到一个比较直观的理解线性变换的方法可以把前面一个矩阵当作两个列向量也就是基向量，后面一个向量当作系数 $[\begin{array}{cc} a & b \\ c & d \end{array}] [\begin{matrix} x \\ y \end{matrix}] = x [\begin{matrix} a \\ c \end{matrix}] + y [\begin{matrix} b \\ d \end{matrix}] = [\begin{matrix} a x + b y \\ c x + d y \end{matrix}]$ 可以把前面的一个矩阵理解成 $[\vec{i} \vec{j}]$

再多一个矩阵来看，就是对基向量多了一次线性变换（不过要从右往左运算）

经过旋转矩阵 $\vec{i} a n d \vec{j}$ 分别变成了 $[\begin{array}{cc} 0 \\ - 1 \end{array}]$ 和 $[\begin{array}{cc} - 1 \\ 0 \end{array}]$ ，然后再分别对这两个基向量左乘剪切矩阵，同理就可以得到上述复合矩阵的两个列向量。

把视野扩大到三维空间，就可以得到：

[\begin{array}{ccc} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{array}] [\begin{matrix} x \\ y \\ z \end{matrix}] = x [\begin{matrix} 0 \\ 3 \\ 6 \end{matrix}] + y [\begin{matrix} 1 \\ 4 \\ 7 \end{matrix}] + z [\begin{matrix} 2 \\ 5 \\ 8 \end{matrix}]

左边的是线性变换矩阵， $[x y z]^{T}$ 是输入向量，得到的结果就是输出向量。

矩阵乘法的规律

从上面的应用可以形象地想象出，矩阵相乘是满足结合律的: 因为从右往左看，基向量 $[\begin{array}{cc} 1 \\ 0 \end{array}]$ 和 $[\begin{array}{cc} 0 \\ 1 \end{array}]$ 经历的变换的顺序仍然是不变的。

(A B) C = A (B C)

而对于矩阵的运算，交换律是不适用的。

M_{1} M_{2} \neq M_{2} M_{1}

可以用图像来理解这一过程：

逆矩阵

引入：线性方程组的计算

\begin{matrix} 2 x + 5 y + 3 z = - 3 \\ 4 x + 0 y + 8 z = 0 \\ 1 x + 3 y + 0 z = 2 \end{matrix} ⟶ [\begin{array}{ccc} 2 & 5 & 3 \\ 4 & 0 & 8 \\ 1 & 3 & 0 \end{array}] [\begin{matrix} x \\ y \\ z \end{matrix}] = [\begin{matrix} - 3 \\ 0 \\ 2 \end{matrix}]

$A \vec{x} = \vec{v}$ 要求解对应的 $\vec{x}$ 就要知道 $A^{- 1} \vec{v}$ 的值。计算方法分为：行列式为 0 和行列式不为 0

$d e t (A) \neq 0$

此时在二维或三维空间中并没有被压缩为面积或体积为 0 的区域。可以找到唯一的解向量 $\vec{x}$ ，使它经过线性变换后与 $\vec{v}$ 重合 (存在唯一解)

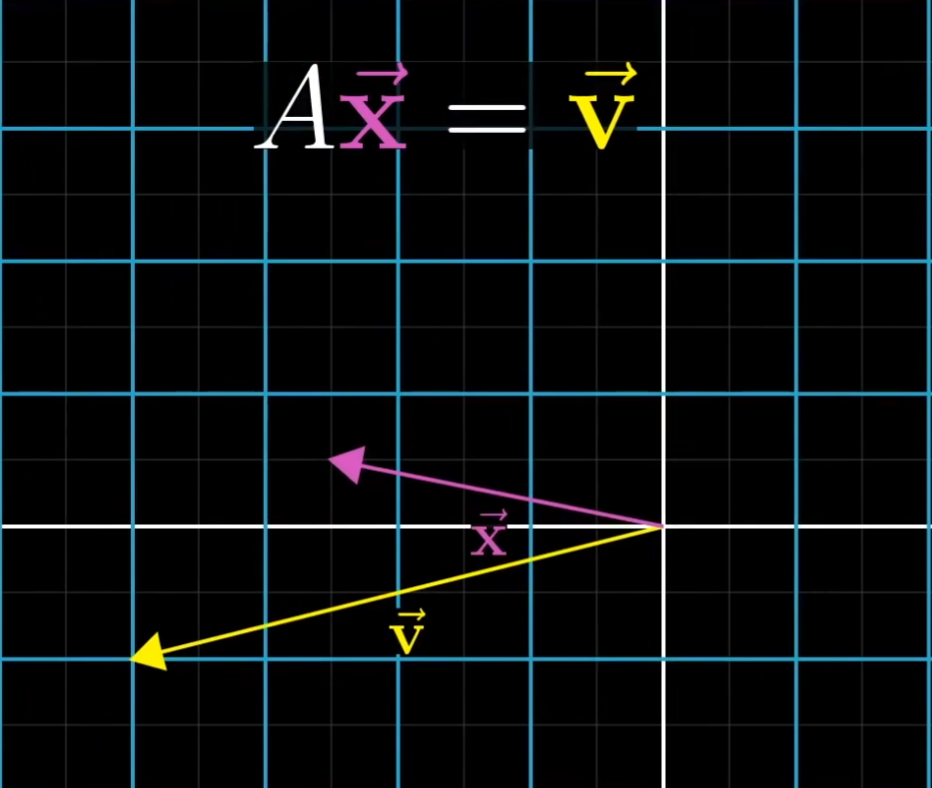
找逆矩阵的过程就是让基向量不发生任何变化，即 $A^{- 1} A = d o e s n o t h i n g$

$d e t (A) = 0$

当矩阵空间可以被压缩到更低维度时，它的行列式为 0，那么不存在一个逆矩阵可以使它提升到更高的维度。（例如从一根直线变换到一个平面）

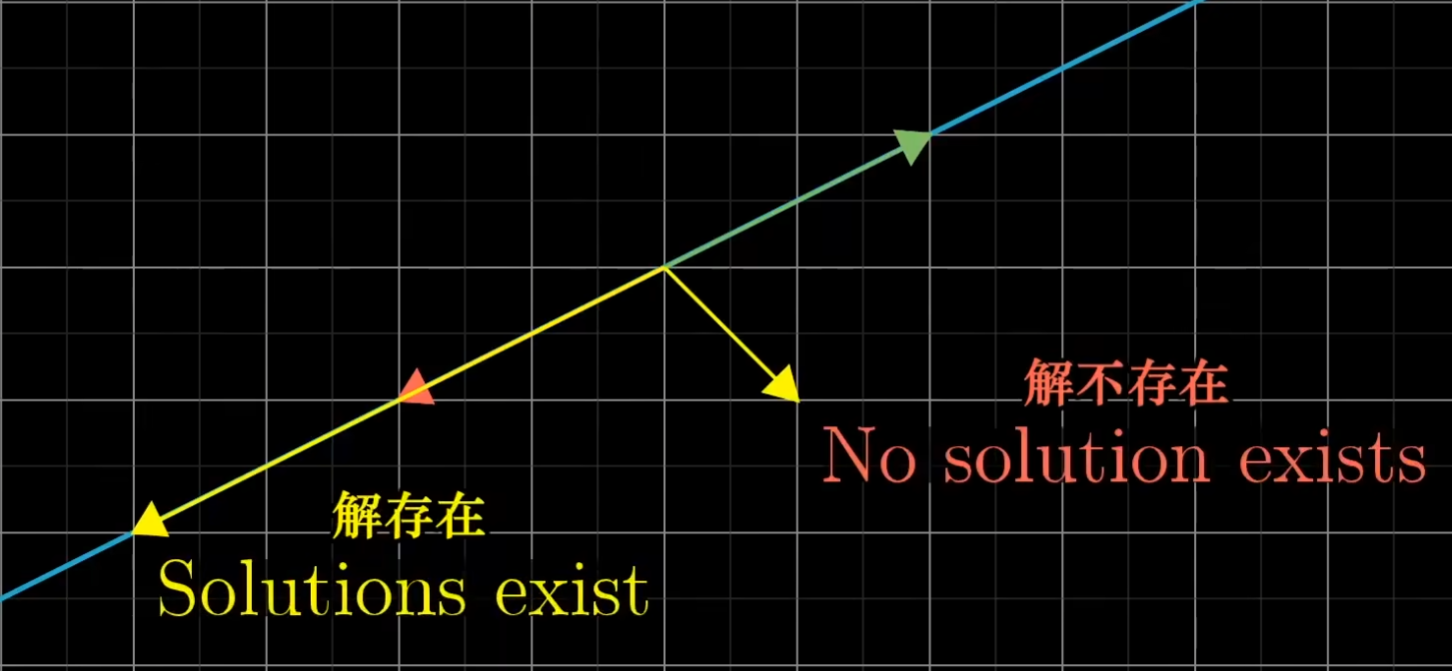
此时解存在 0 个或无数个。

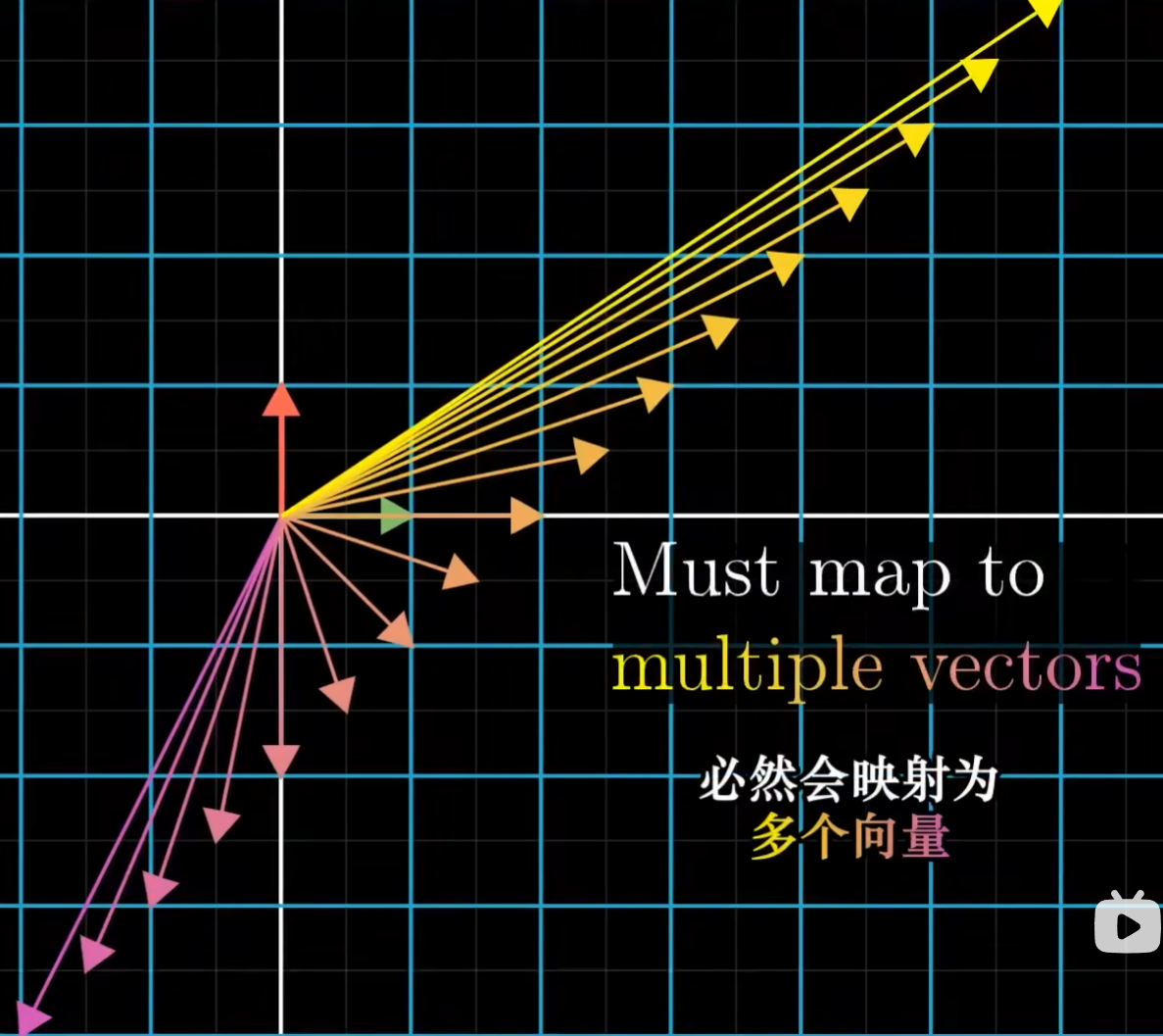
秩（rank）

秩的定义是变换后空间的维数

Rank is the number of dimensions in the output

零空间（Null space）

一些向量变换后落到零向量上，这些向量构成的空间就是零空间。

贡献者

OveDuke

文件历史

最后编辑于 2 天前查看完整历史

矩阵向量的乘法 ​

矩阵乘法的规律 ​

逆矩阵 ​

引入 ：线性方程组的计算 ​

det(A)≠0 ​

det(A)=0 ​

秩（rank） ​

零空间（Null space） ​

贡献者 ​

文件历史 ​