字数
355 字
阅读时间
2 分钟
点乘 (dot product)
对于两个维数相同的向量,点积就是对应项相乘再相加。 例如:
点乘的几何的意义
几何的意义:向量的点乘就是: (一个向量的长度) 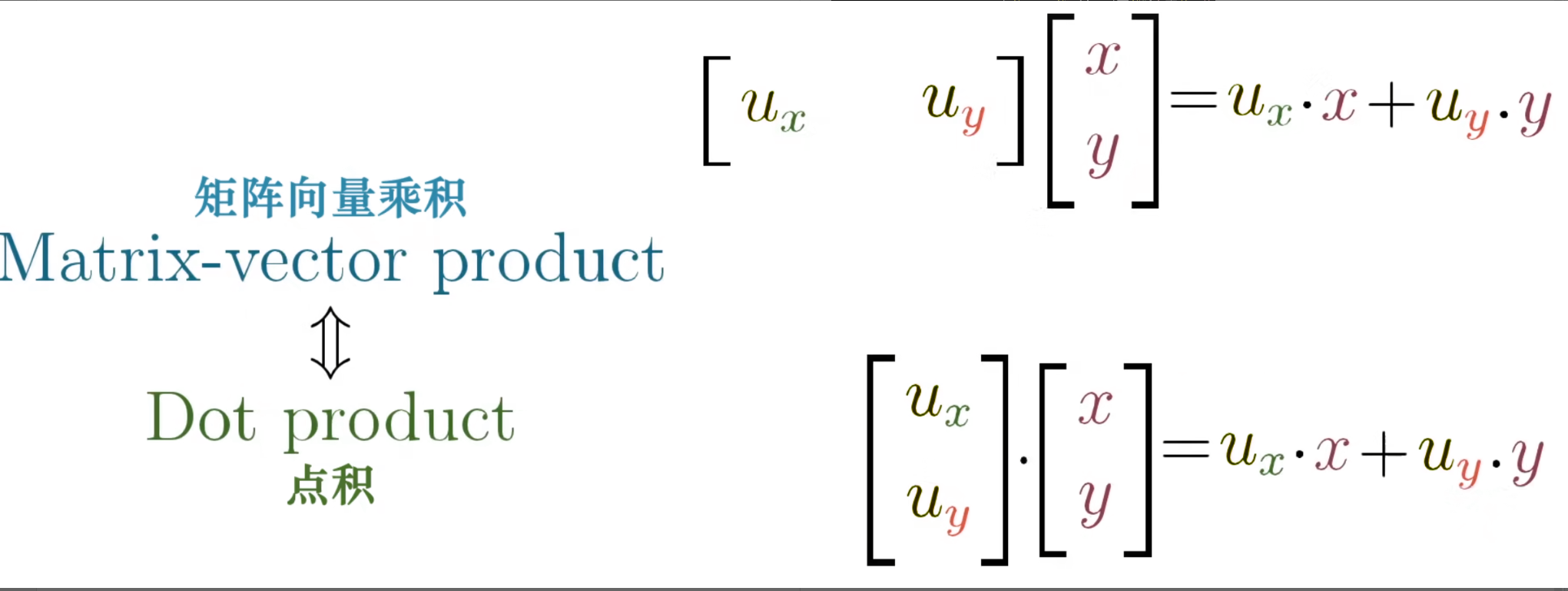 与单位向量的点积等于将向量投影到单位向量所在的直线上所得到的投影长度
与单位向量的点积等于将向量投影到单位向量所在的直线上所得到的投影长度 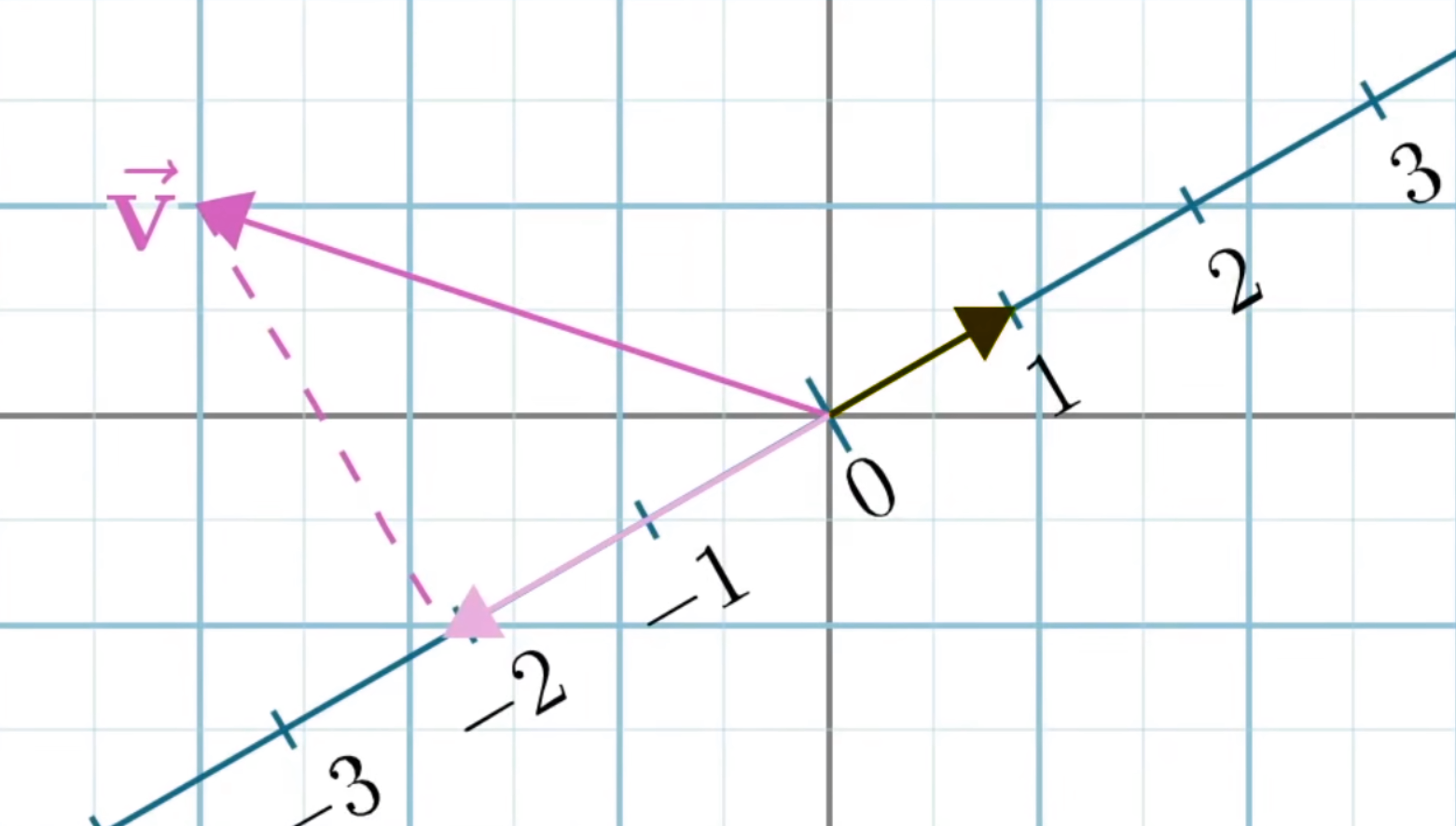
叉乘 (cross product)
叉乘的方向
两个向量的叉积仍然是向量。 方向的确定满足右手定则 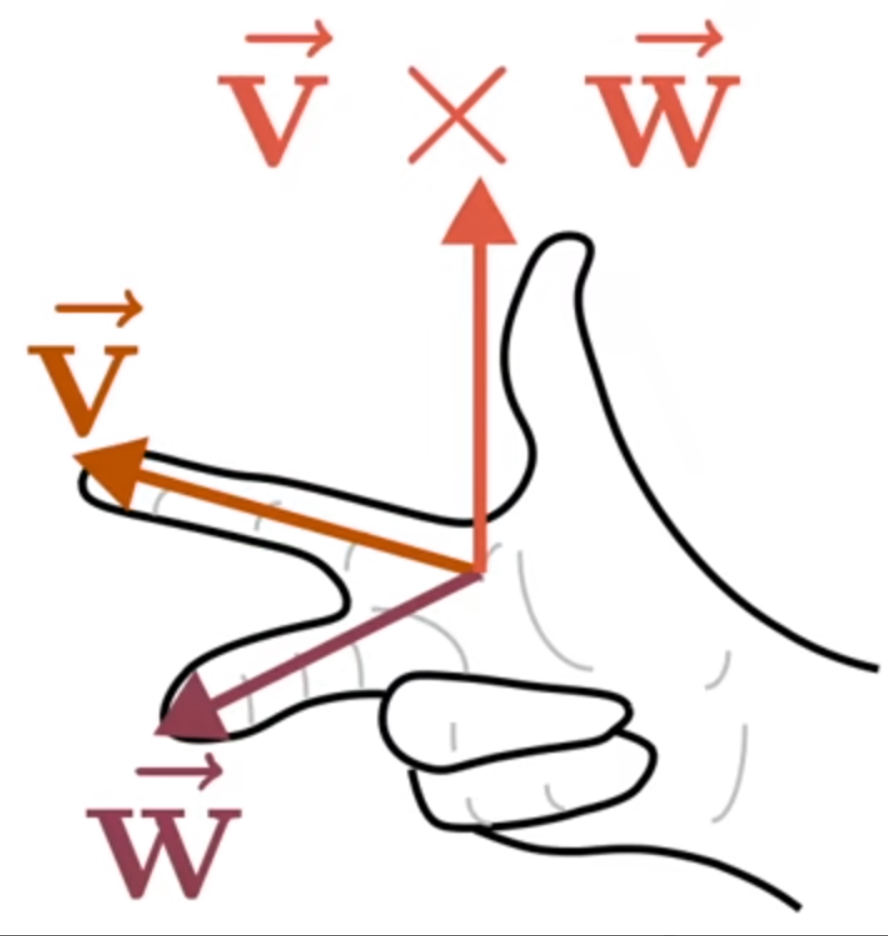
叉乘的大小
两个向量叉乘的大小就是两个向量所围成的平行四边形的面积。
正负由方向决定,对于
当 沿逆时针方向扫到 ,结果为正。当顺时针扫过,结果为负。
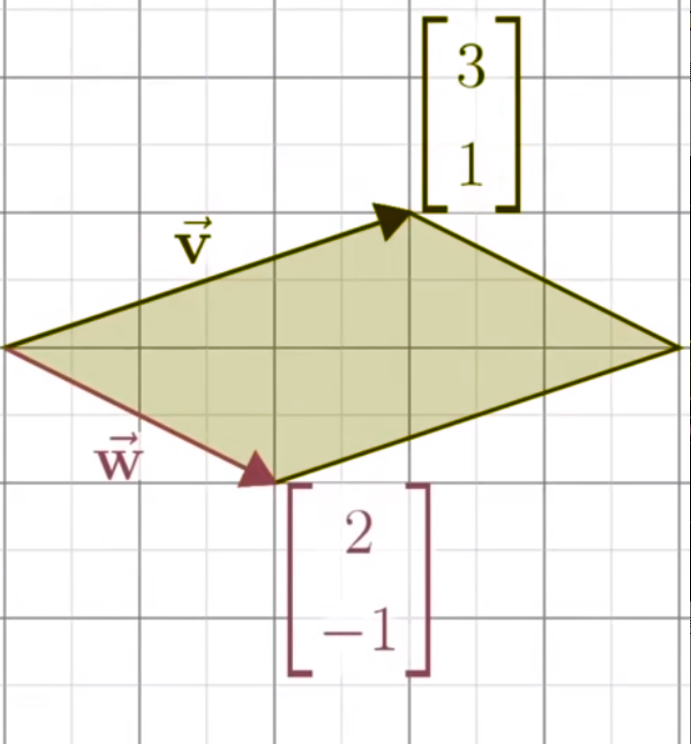 可以联想到行列式的几何意义
可以联想到行列式的几何意义
叉乘向量
叉乘向量的计算公式如下:
如何记忆? 可以按照如下的方法记忆:
计算就可以得到各个基向量的系数