Notebase

字数

346 字

阅读时间

2 分钟

行列式计算值的意义就是将基向量围成的面积缩放的比例。 ^2b4950

例如：原本基向量 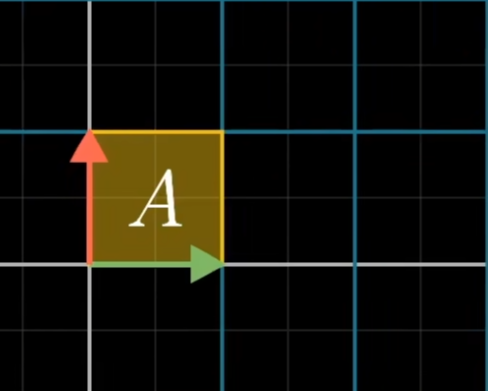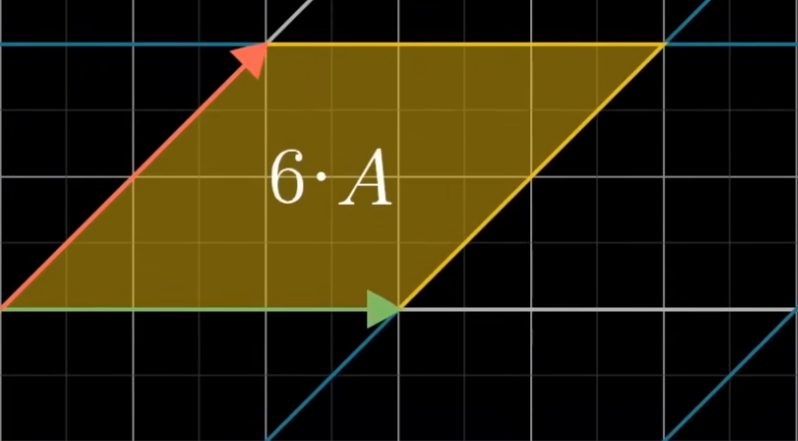$[1 0]^{T}$ 和 $[0 1]^{T}$ 经过左乘变换矩阵 $[\begin{array}{cc} 3 & 2 \\ 0 & 2 \end{array}]$ 后会发生如下的变化，面积的缩放比例正是该变换矩阵的值。下面的例子同样可以解释：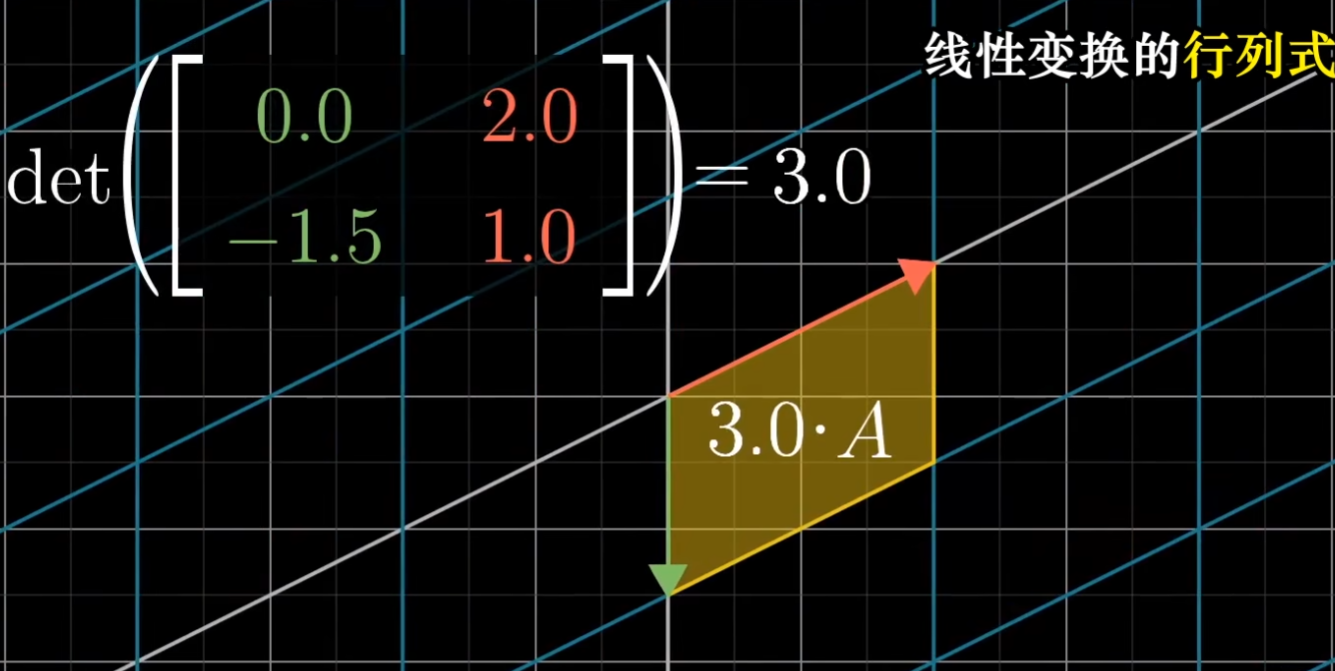

这是一个特殊的例子，当两个基向量共线时，面积被压缩为 0：这在逆矩阵中会用到 ^a0c35c

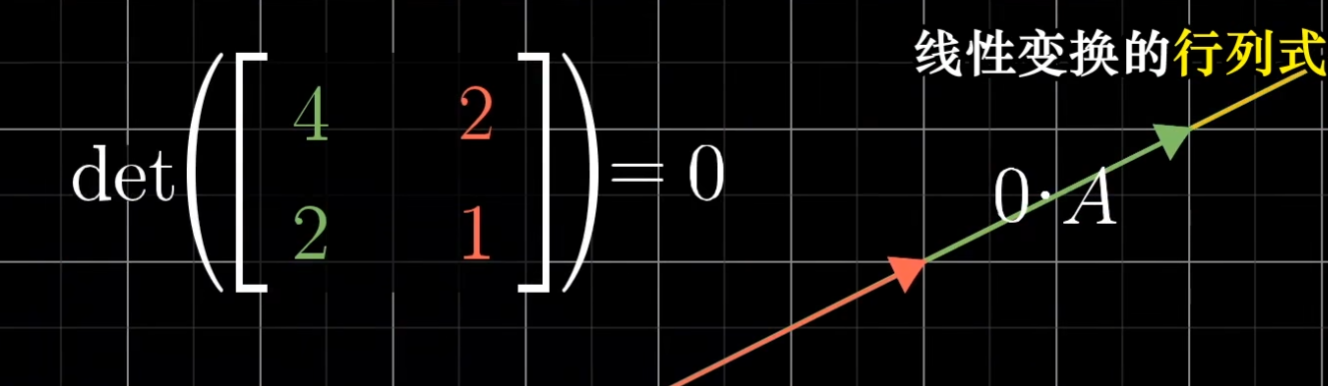
如果行列式的值为负值，意味着定位发生变换，就好比是从平面的正面翻转到反面

对于三维空间，行列式的值就是将基向量围成的体积缩放的比例。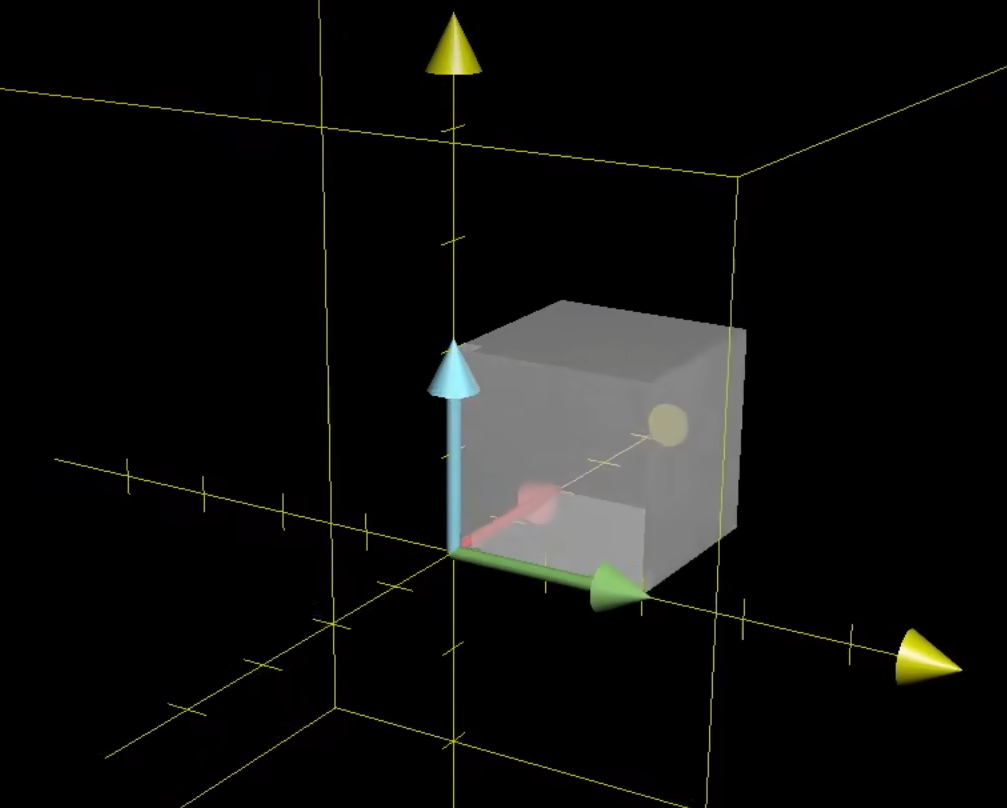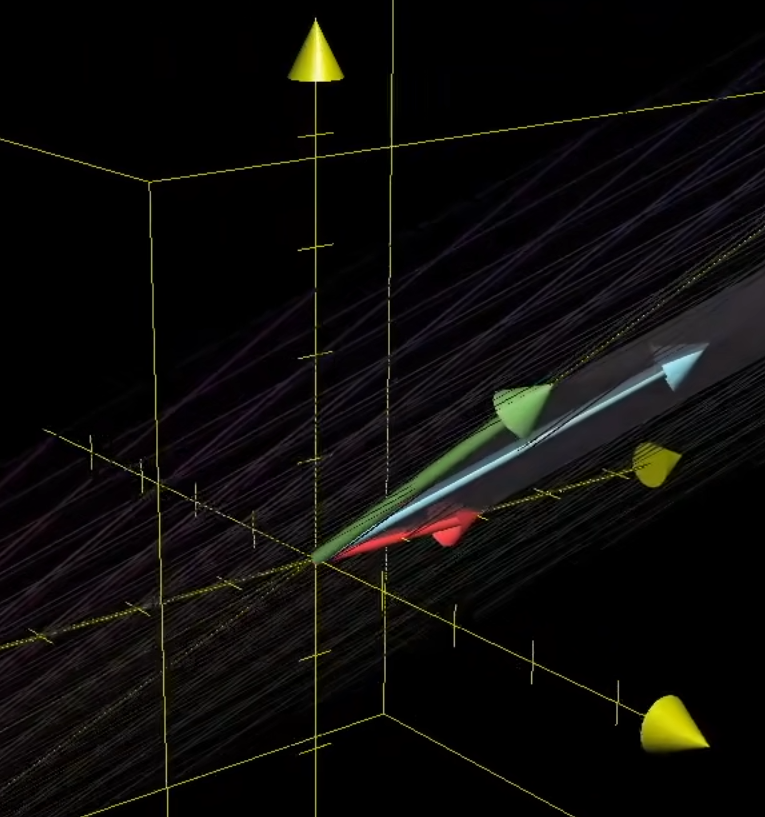当一个 $3 \times 3$ 的行列式值为 0 时，意味着这个三维空间被压缩为一个平面、一条直线或是一个点。（也就是空间被压缩到了更低的维度）

det ([\begin{matrix} 1.0 & 0.0 & 1.0 \\ 0.5 & 1.0 & 1.5 \\ 1.0 & 0.0 & 1.0 \end{matrix}]) = 0

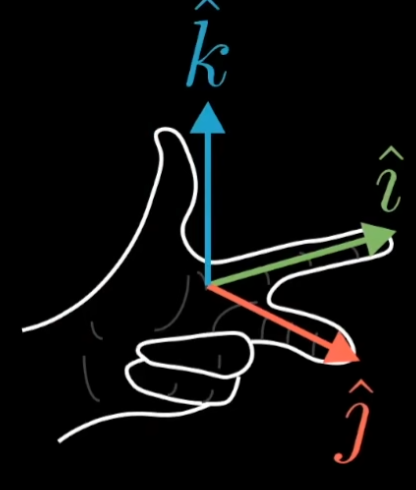
如果行列式的值为负值，意味着定位发生变换，将从右手系变为左手系。

det (M_{1} M_{2}) = det (M_{1}) \det (M_{2})

计算机图形学，机器人学

贡献者

OveDuke

最后编辑于 2 天前查看完整历史