字数

988 字

阅读时间

5 分钟

同章节文件

2_1采样定理 2_2常用信号

生成仿真信号

1 正弦累加周期信号

先使用下面的函数生成时间间隔和对应的采样点数值。 然后 tfrstft (t, y, fs) 函数通过输入采样点和采样频率，绘制出时域波形和时频分布图。

function [ output_args ] = example2_9( input_args )
clc;
clear;
fs=256;
f1=25;
f2=100;
t=0:1/fs:1-1/fs;
y=sin(2*pi*f1.*t)+2*sin(2*pi*f2.*t);
tfrstft(t,y,fs)
end

下面是 tfrstft(t,y,fs) 函数

function [ output_args ] = tfrstft(t, y,fs )
% 绘制时域波形
figure;
subplot(2,1,1);
plot(t, y);
title('时域波形');
xlabel('时间 t/s');
ylabel('幅值');
grid on;
% 计算并绘制时频分布图 (使用 spectrogram 函数)
% 注意：spectrogram 的参数可以根据需要调整
[~, F, T, P] = spectrogram(y, hamming(32), 16, 128, fs, 'power');
% 应用阈值
% P(P < max(P(:))*0.02) = NaN;%可以应用阈值进行筛选
subplot(2,1,2);
surf(T, F, 10*log10(abs(P)), 'EdgeColor', 'none');
view(0, 90); % 设置视角为顶视图
colorbar;
title('时频分布图');
xlabel('时间 t/s');
ylabel('频率 f/Hz');
zlabel('功率谱密度 (dB)');
shading flat;
end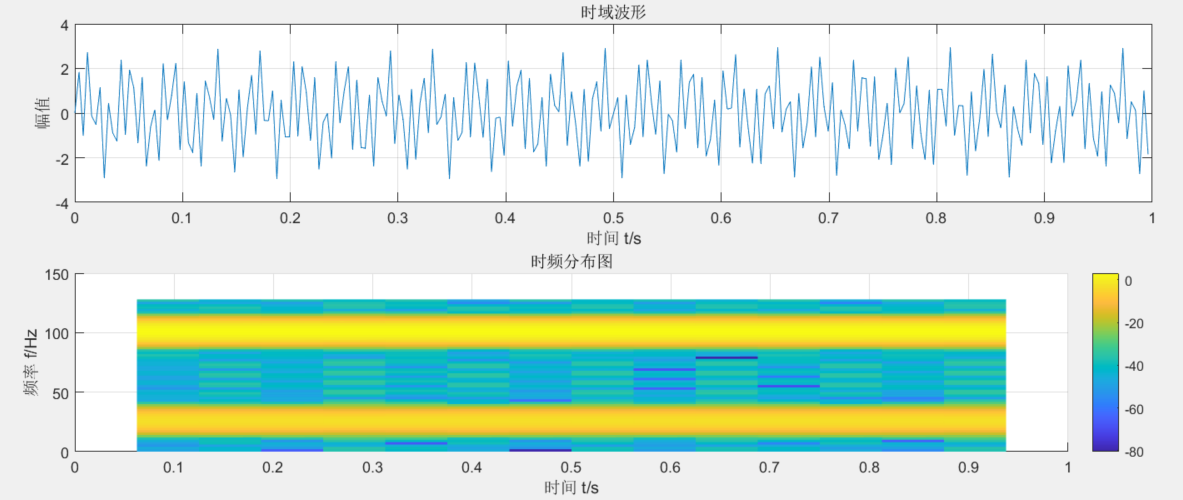

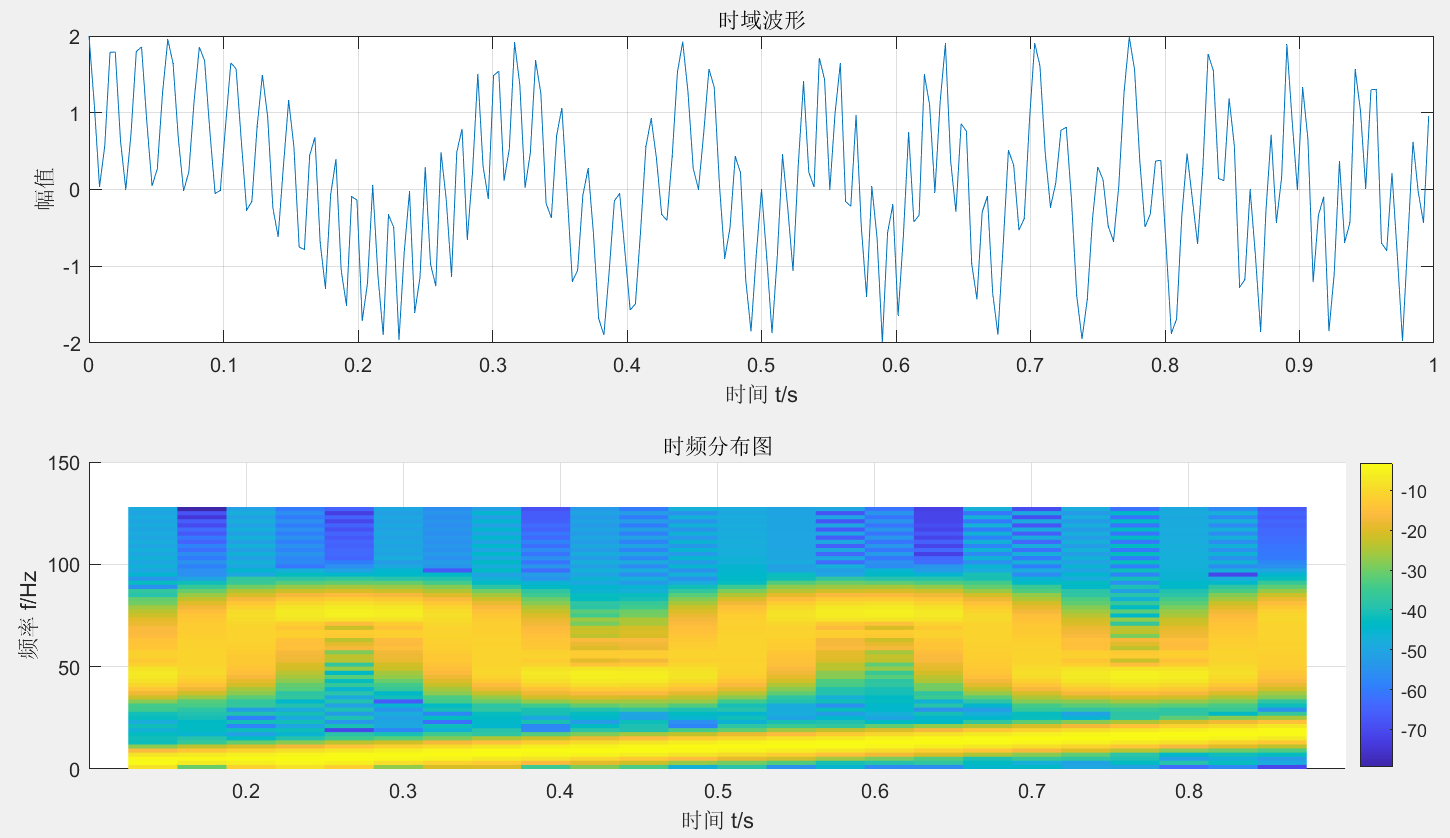
2 调频累加信号

通过下面的函数生成一个调频累加信号。

function [ output_args ] = example2_10( input_args )
clc;
clear;
fs=256;
t=0:1/fs:1-1/fs;
y=cos(20*pi.*t.*t)+cos(2*pi.*cos(6*pi.*t)+120*pi.*t);
tfrstft(t,y,fs);
end

tfrstft(t,y,fs) 的定义同上。 其中spectrogram函数设置如下： [~, F, T, P] = spectrogram(y, hamming(64), 56, 128, fs, 'power')

3 周期性振动冲击信号

function [ output_args ] = example2_11( input_args )
clc
clear 
fs = 20e3;                 % 采样频率
fn = 3e3;                  % 固有频率
y0 = 3;                    % 位移常数
g = 0.1;                   % 阻尼系数
T = 0.02;                  % 重复周期
N = 4096;                  % 采样点数
NT = round(fs*T);      % 单周期采样点数
t = 0:1/fs:(N-1)/fs;      % 采样时刻
t0 = 0:1/fs:(NT-1)/fs;  % 单周期采样时刻
K = ceil(N/NT)+1;       % 重复次数
y = [];
for i = 1:K
    y = [y,y0*exp(-g*2*pi*fn*t0).*sin(2*pi*fn*sqrt(1-g^2)*t0)];
end
y=y(1:N);
tfrstft(t,y,fs)
end

y0*exp(-g*2*pi*fn*t0)：这部分表达式描述了==指数衰减包络线== sin(2*pi*fn*sqrt(1-g^2)*t0)：这部分是一个==正弦波，表示振荡部分==。2*pi*fn 给出了角频率，sqrt(1-g^2) 是对频率进行调整以考虑阻尼效果，因为实际振荡频率会在一定程度上低于无阻尼情况下的固有频率。

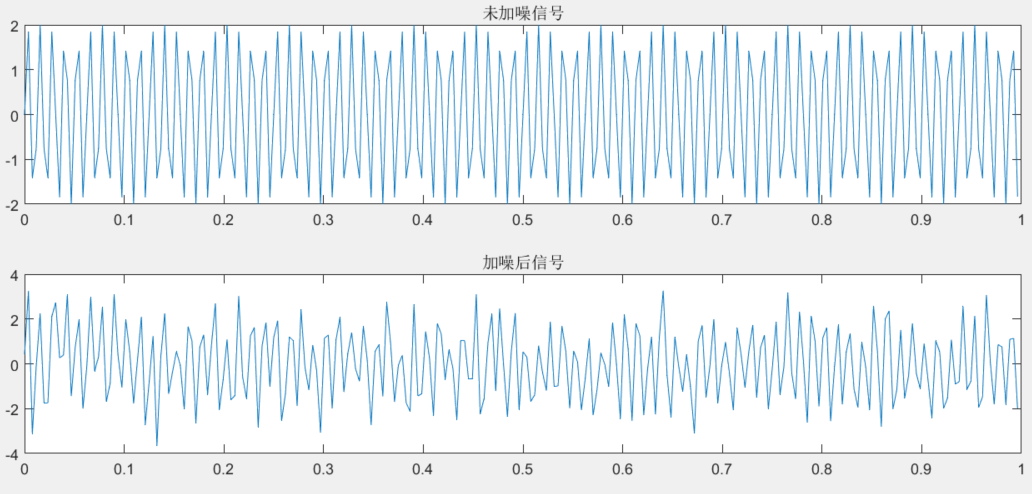
4 加噪信号

正弦波信号中添加高斯白噪声 什么是信噪比？Ai(通义)-信噪比

function [ output_args ] = example2_12( input_args )
clc; % 清除命令窗口
clear; % 清除工作空间中的所有变量

fs=256; % 采样频率为256 Hz
f1=80; % 正弦波的频率为80 Hz
t=0:1/fs:1-1/fs; % 创建时间向量，从0到1秒（不包括1秒），步长为1/fs

sig=2*sin(2*pi*f1.*t); % 生成振幅为2、频率为80 Hz的正弦波信号

SNR=5; % 设置信噪比(SNR)为5 dB

NOISE=randn(size(sig)); % 生成与信号大小相同的高斯白噪声
NOISE=NOISE-mean(NOISE); % 将噪声均值调整为0

signal_power=1/length(sig)*sum(sig.*sig); % 计算信号的平均功率
noise_variance=signal_power/(10^(SNR/10)); % 根据SNR计算噪声方差

NOISE=sqrt(noise_variance)/std(NOISE)*NOISE; % 调整噪声的标准差以满足指定的SNR
%std是MATLAB中的一个函数，用于计算数据的标准差，它衡量的是数据点相对于平均值的离散程度。
%sqrt(noise_variance)，标准差是方差的正平方根
%这部分是一个比例因子，用来调整原始噪声的标准差，使得调整后的噪声具有期望的标准差。
y=sig+NOISE; % 向原始信号中添加噪声

figure(1) % 创建一个新的图形窗口或激活编号为1的窗口
subplot(211) % 在图形窗口中创建两个子图中的第一个
plot(t,sig); % 绘制原始信号
title('未加噪信号'); % 添加标题

subplot(212) % 创建两个子图中的第二个
plot(t,y); % 绘制加噪后的信号
title('加噪后信号'); % 添加标题
end

贡献者

OveDuke

文件历史

最后编辑于 34 分钟前查看完整历史

7088e-update_matlab_faults